三角形の2辺の長さと直角ということを利用し、残りの角のひとつを出したいと考えています。 やり方として、三平方の定理で角度を出す、「COSθ=b/a」 (b,aは三角形の辺の長さです) を使用してやろうと考えております。 その角度θを今プログラム的に求め次に㋑を求めてみます。 右の図で三角形fpdに着目すると、三角形の内角の和は180°だから、 180°-(70°+90°)=° で、角fpdは°です。 さらにpに着目して、直線の角は180°であることより ㋑+90°+° =180°だから ㋑=70° となります。 三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135° x=135°-60°=75°

中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
三角形の角度の求め方 中学生
三角形の角度の求め方 中学生- 三角形の内角と外角の関係から ● = ○ + ● 角A=30°+90°=1° 二等辺三角形の角度の問題では 底角が等しいこと 三角形の外角の性質 この2点を覚えておけば応用問題でも解くことができます。 ただし、発想が難しい問題もあるので、いろんな問題集を使って知識を深めておきましょう。 スポンサーリンク



普通の電卓で計算できる直角三角形の近似計算
この問題を見て,逆三角関数 tan1 (C言語では atan() や atan2()) を使って CP と CQ の角度をそれぞれ求め, 両者を比較しようと考えた方が多いのではないでしょうか. しかしこの問題では,角度そのものではなく角度差の符号を求めればよいので, 逆三角関数を使う方法よりも簡単で優れた,外積 三角形の角度 三角形の内角の和は180 三角形の面積の求め方は「底辺×高さ÷2」ですから、 答え)50cm 2 右側の直角二等辺三角形はどうでしょう? 考えてみましょう。 分かりましたか 1 三角関数の角度の求め方、三角方程式の解き方 2 三角関数の角度を求めるsin編 21 三角関数の角度sinを求める①:単位円を利用する 22 三角関数の角度sinを求める②:sinθ=aのときy=aをグラフに書く
一方、三角形の内角の和は 180 ∘ なので、 ∠ B ∠ C = 180 ∘ − 40 ∘ = 140 ∘ 下の四角形のaの角度を求めなさい。 解説 下の図のように四角形の1本の対角線で2つの三角形に分けます。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでaの角度は、360°(72°38°30°)=2° よって、 答え a=2 °解説 ≪三角比の値の求め方≫ sinθ,cosθ,tanθの値は,次の「よく出る2つの三角形」と「sinθ,cosθ,tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。
三角比の辺の比率について、下の図を使って説明します。 2つの三角形の左端の角度を見てください。 それぞれの角度は、30度の直角三角形と45度の直角二等辺三角形です。 いろいろある角度の中でこの30度と45度の角度の時は、人が覚えやすい比率になり鋭角の三角比 §2 三角比 2.鋭角の三角比 ここでは,前の章で説明した三角比の定義だけでは,まだ理解できないと思いますので,いろいろな三角形を用いて三角比の定義の理解を深めていくことにしましょう。 そこで,もう一度,三角比の定義のお この記事では、三角関数について、角度の求め方や変換公式(\\(90^\\circ − \\theta\\) など)について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいね!




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座
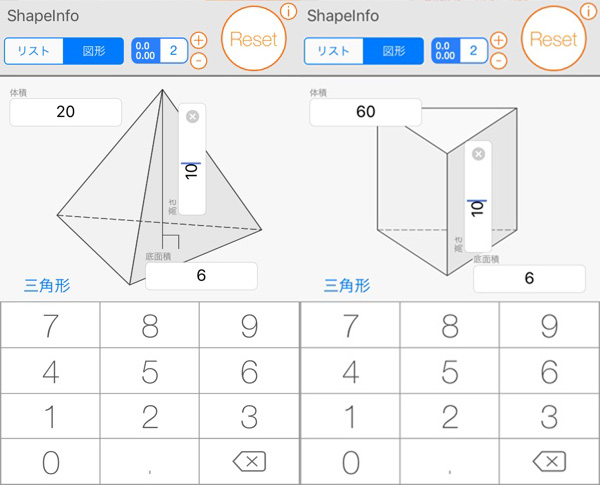



三角形や球も 様々な図形の面積や角度がすぐに分かる 図形電卓 が超便利 Isuta イスタ 私の 好き にウソをつかない
正多角形の内角・外角の求め方を解説!←今回の記事 星形の角度の求め方を解説! ブーメラン型の角度の求め方! ちょうちょ型の角度の求め方を解説! 合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法!/ 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c, sinθ= b c, tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。



2 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に




角度の求め方 算数の教え上手 学びの場 Com
・直角三角形(高さと斜辺) 直角三角形の高さと斜辺から、底辺と角度と面積を計算します。 ・直角三角形(高さと角度) 直角三角形の高さと角度から、底辺と斜辺と面積を計算します。頂角の求め方、二等辺三角形との関係 頂角の求め方を下式に示します。 頂角=180°-2×底角 三角形の内角の和は180°です。2つの底角の角度は等しいので180°から底角の2倍を引いた値が頂角となります。 下図の二等辺三角形の頂角を求めてください。 (1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。
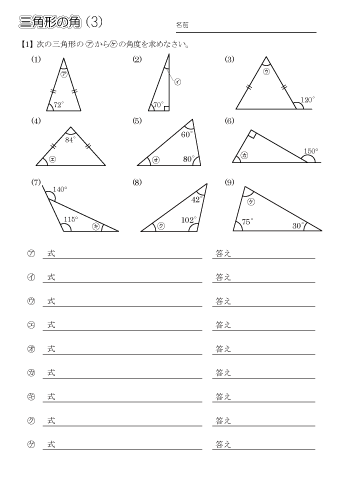



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。直角三角形の角度の出し方を教えてください!! 直角三角形で、3辺の長さがわかっている場合に残り2つの角度の出し方を教えてください!!①電卓がある場合(関数機能のないもの。ルート機能だけある Read 523 直角三角形の角度の求め方 教えて下さい。三角形の形状問題 三角形の証明問題 内接円の半径 正弦・余弦・面積 (センター問題) 三角比のセンター試験問題 → スg スム版は別包ソス ス ス スO スモ ソス スp スs ス ス スt ス ス ス@ ス ス ス ス阯晢ソス@ ス ス スQ ス ス ス ス スQ ス ス スQ 2 ス ス
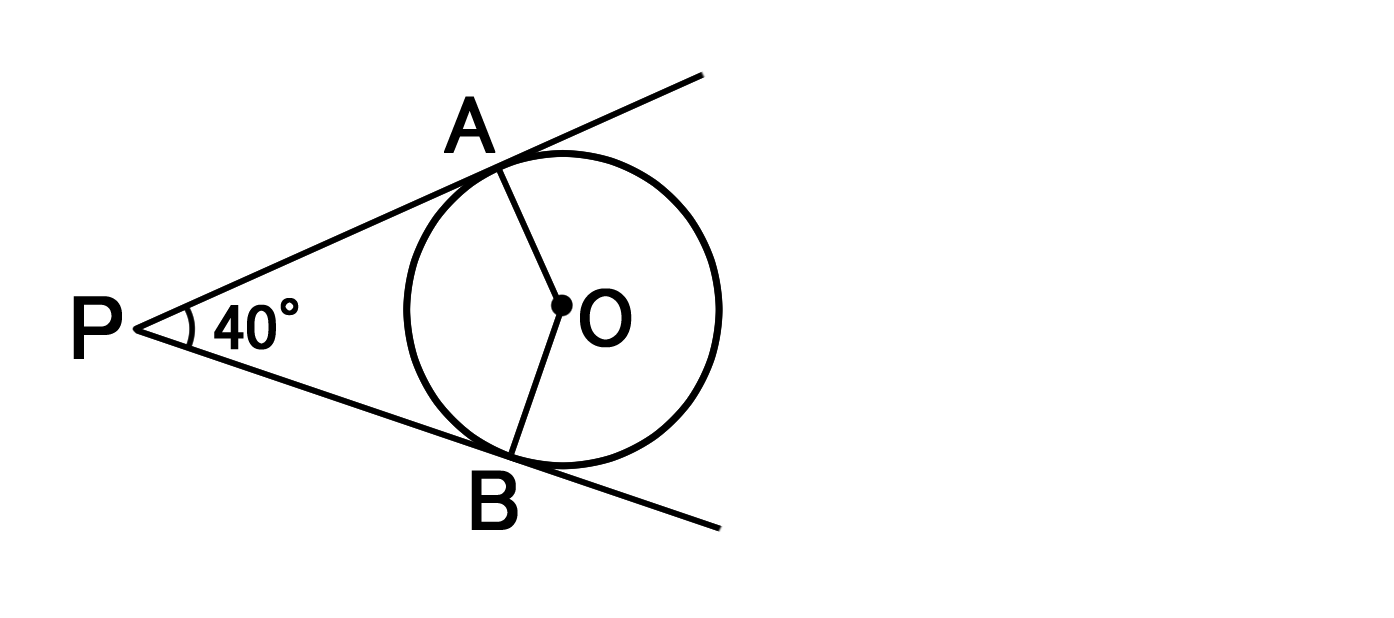



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学




二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思うので教え Clear
小学校5年生で習う「三角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに三角形の内角の角度の求め方についてはこちらに詳しく説明しています。 三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦(cos(コサイン))を求める。三角形、四角形、角、面積 円、三角形、四角形の面積を計算できるようになろう。 角度のはかり方もいっしょにおぼえてね。 動画で学ぼう! (NHK for School) 三角形の面積の求め方を、四角に直すことで原理から考える。 結婚式場から指輪が盗まれた




中学2年生の角度を求める問題です 娘に質問されて答えられませんでした Okwave




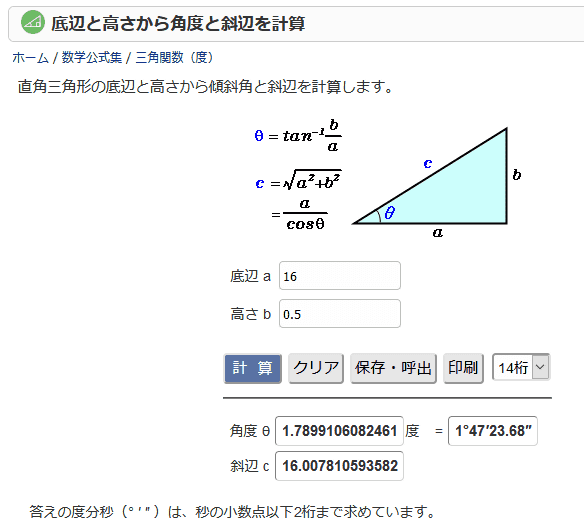
底辺と高さから角度と斜辺を計算 高精度計算サイト
直角三角形の角度の求め方 こんにちは! 大神です。 今日は学校の 勉強は大事だよ ということを書いていこうと思います。 突然ですが皆さんは 「直角三角形の角度の求め方」 の公式を覚えていますでしょうか? サイン・コサイン・タンジェント答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を 多角形の内角の和の公式 三角形の内角の和: 180° 180 ° 四角形の内角の和: 360° 360 ° 五角形の内角の和: 540° 540 ° 六角形の内角の和: 7° 7 ° ・・・ n角形の内角の和: 180°× (n−2) 180 ° × ( n − 2 ) この公式は覚えやすいので暗記してもいい




二等辺三角形の角を求める Youtube




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト
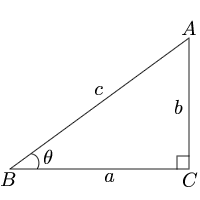
三平方の定理 225°,\ 675°の三角比は数II}で半角の公式を学習すると割と容易に求められる よって,\ 15°,\ 75°の三角比と同じく参考程度の問題である まず,\ 各辺の長さをすべて求める\ 本問の2重根号ははずせない このため,\ 有理化を含めた式変形が厄介斜辺の長さをr,他の辺の長さをx,y とするとき, y r, x r, y x, の値は,三角形の大きさに関係なく,角θの大きさだけで決まる。 これらを,それぞれθの 正弦(sine), 余弦(cosine), 正接(tangent) といい,sinθ, cosθ, tanθと表す。まずは、角度Bは簡単に求まります。三角形の内角の和は180度ですから、「C = 180 A B = 180 35 90 = 55」より、角Cの大きさは55度だと分かります。 aとbの求め方 次に、aとbを求めてみま




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



普通の電卓で計算できる直角三角形の近似計算




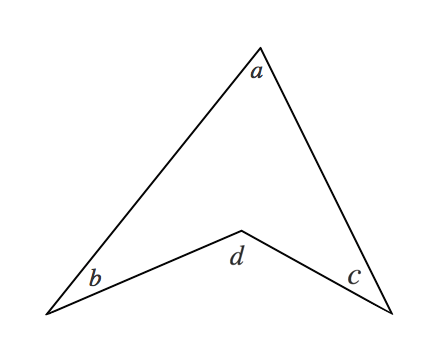
ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく



1




円の中にある二つある三角形の角度の求め方 数学 解決済 教えて Goo
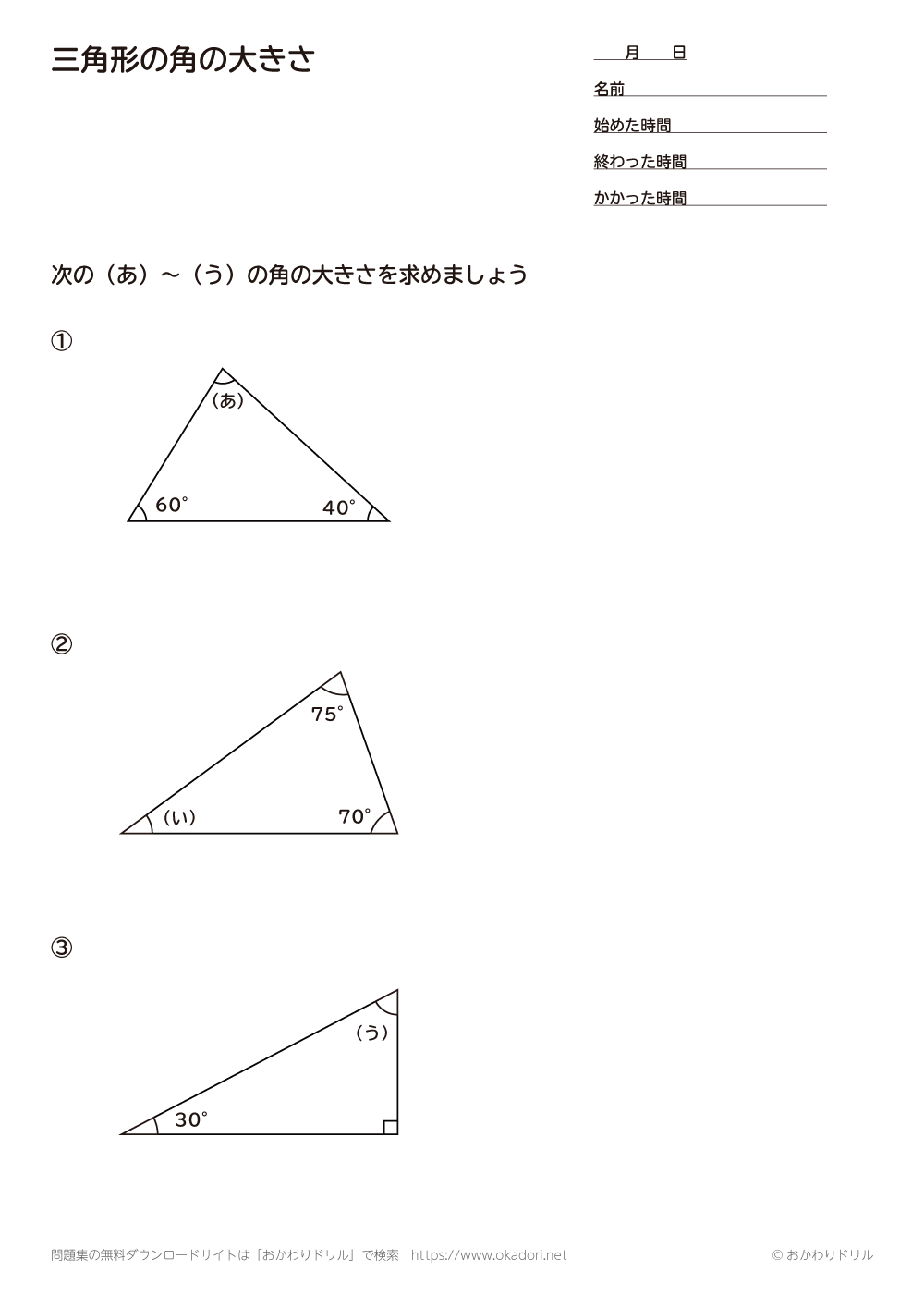



小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



1




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
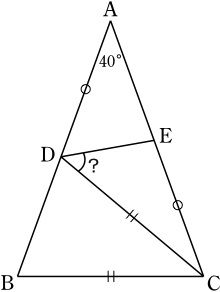



二等辺三角形の頂角を求める問題の 逆 の問題 東大合格コム




角度の計算 裏技まとめ 教遊者



三角関数 1 Cg 数学 06aa



連続する二等辺三角形の角度の法則 算数解法の極意



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ
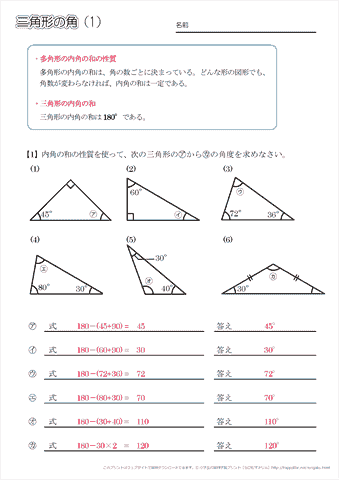



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
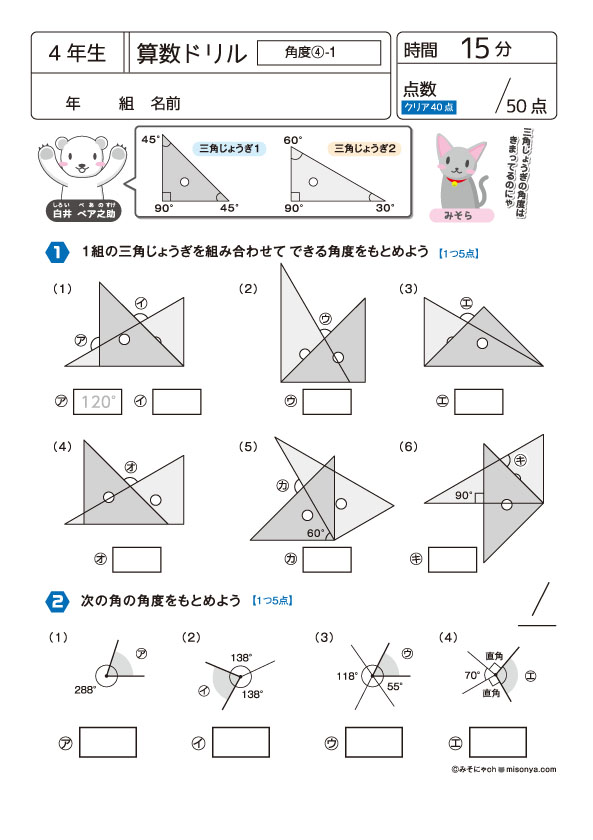



無料の学習プリント 小学4年生の算数ドリル 角度4 総合問題 みそにゃch



ラングレーの問題 整角四角形




角度の求め方 角度の求め方 Mqttk



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



円と三角形 角度 中学から数学だいすき



三角関数から角度 逆三角関数 三角形の計算 計算サイト




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算



中学二年 数学 三角形の角度の求め方 中の上編 Youtube




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




小5 算数 小5 31 三角形の角 Youtube




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学と英語 Note




三角形の辺から角度を計算 製品設計知識
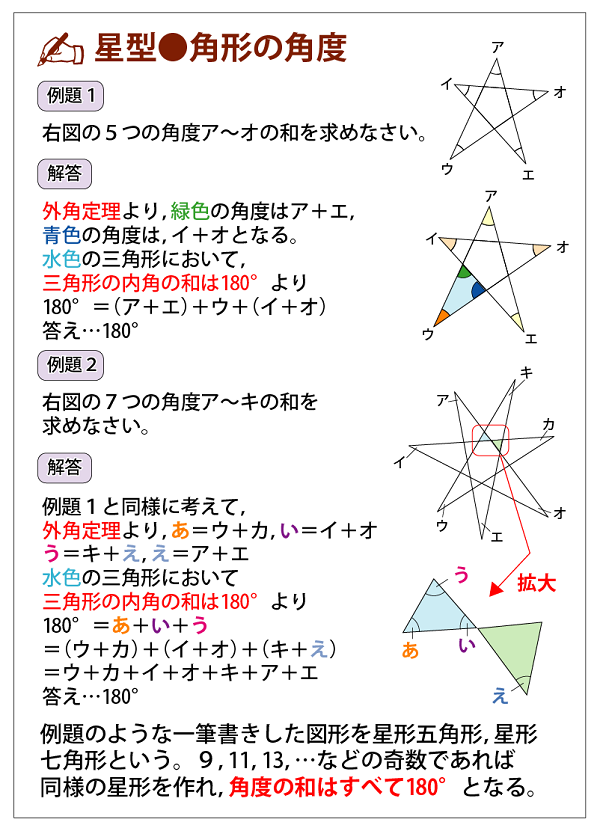



上 図形 角度 求め方




小4算数の角度の問題 折り返し 錯角 同位角で混乱する




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi
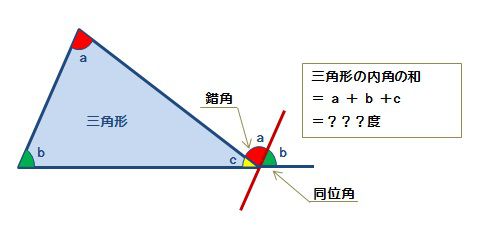



三角形の内角の和 算数の公式覚えてますか




三角形の3辺から角度を計算 高精度計算サイト




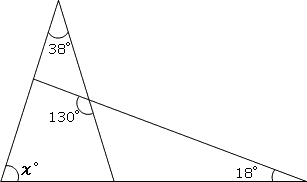
あ かまでの角度を求めてください 急いでます 教えてください Clear




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学



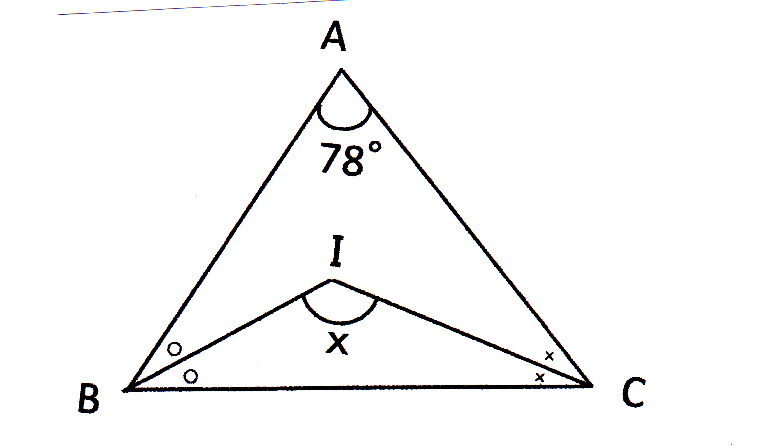
点iはこの三角形の内心である 点iのなすaの角度は何度か 求め方教えて Yahoo 知恵袋
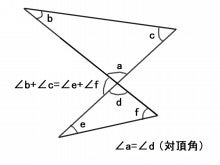



角度の求め方 数学が嫌いなんです
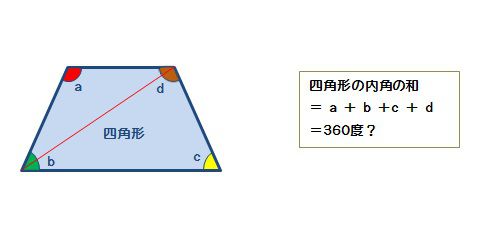



四角形の内角の和 算数の公式覚えてますか
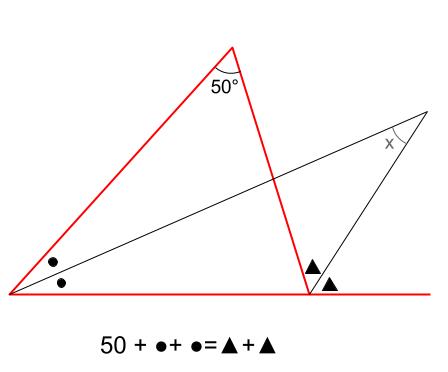



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su




タンジェントとは何か 中学生でも分かる三角関数の基礎




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ
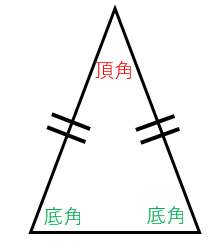



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学



直角三角形の解法 1
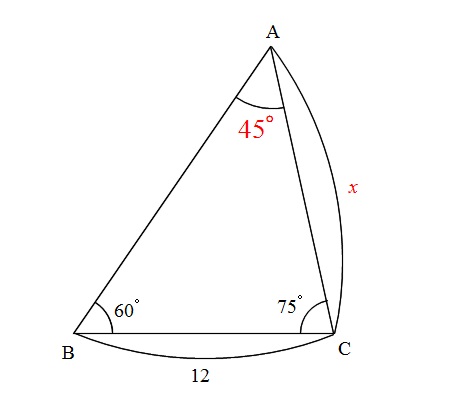



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない



三角形の角度を求める 思考力を鍛える数学




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo
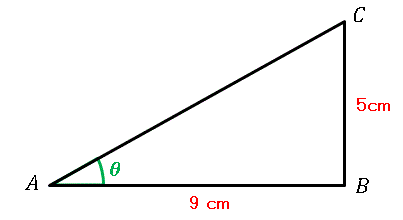



Excel で直角三角形の斜辺と底辺に挟まれた角度を求めます




角度の問題まとめ 無料で使える中学学習プリント



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋
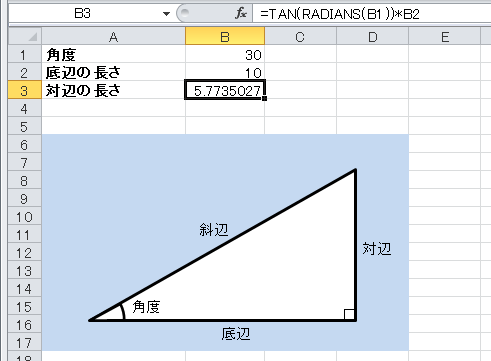



角度からタンジェントを計算するには Tan Radiansの解説 エクセル関数リファレンス




角度の求め方 算数の教え上手 学びの場 Com




角度を計算する方法 9 ステップ 画像あり Wikihow




三角形の角度を求める問題 小学生 中学生の勉強
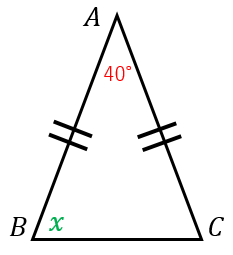



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典




中2数学 ブーメラン型角度の求め方を解説 数スタ



二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明
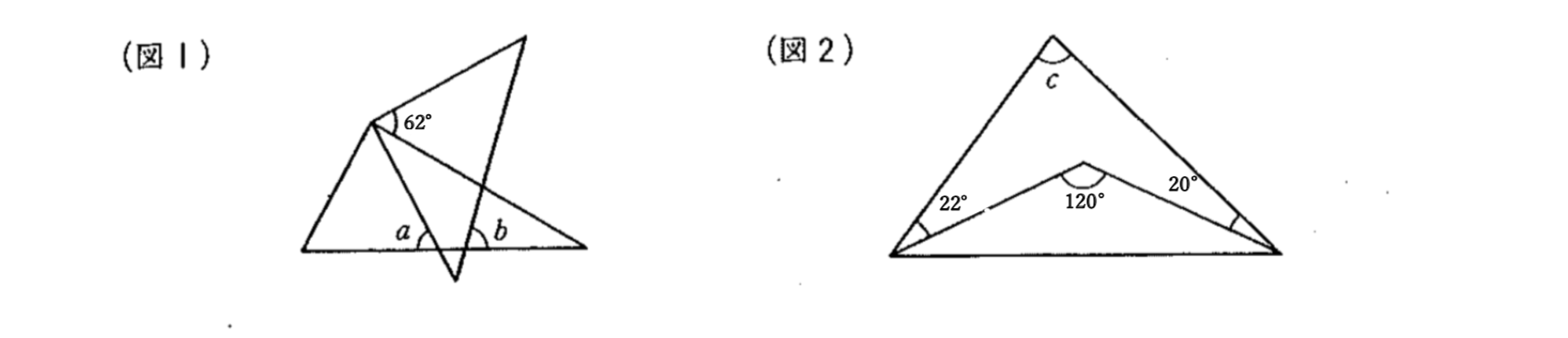



4 3 重なった2つの三角形から角度を求めるには さんすうがく
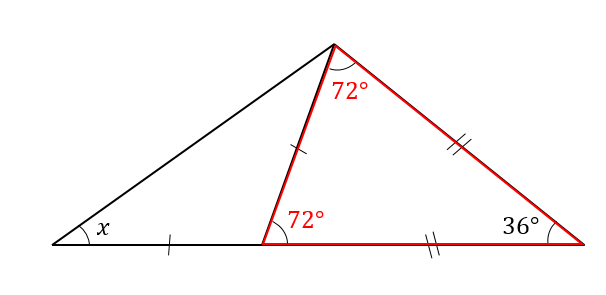



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



角度の求め方 算数の教え上手 学びの場 Com




算数の問題でもあり 数学の問題でもありますの解答解説1 角度を求める問題7月19日出題 Fitのひろば




黄金三角形による18 シリーズの三角比 おいしい数学




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す



表計算ソフトを使って 底辺 と 高さ から 角度 を求める




余弦定理で角度を求める方法 数学の星



角度の難問 中学生版




余弦定理を使った計算 3辺のみが与えられた場合 数学i By Okボーイ マナペディア




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




中2 数学 4 2 三角形の角度の利用 Youtube
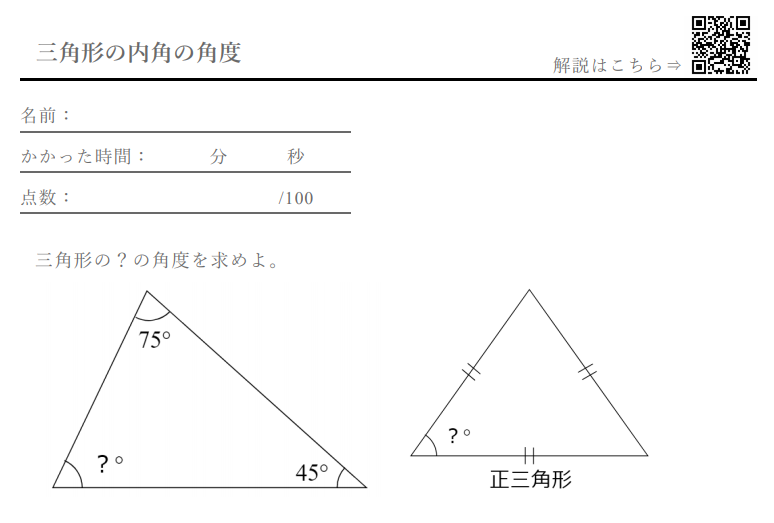



三角形 の内角の角度 計算ドリル 問題集 数学fun
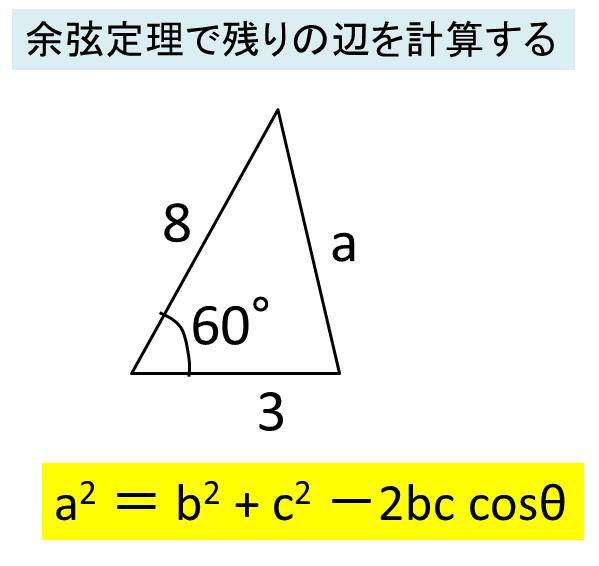



Excel エクセルで余弦定理の計算をする方法 角度や辺の長さを求める
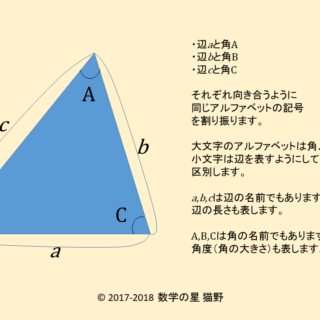



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星
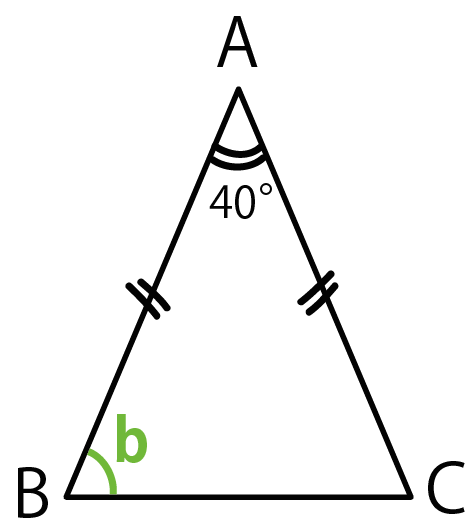



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題



紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター




三角形の角度を求める問題 小学生 中学生の勉強




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
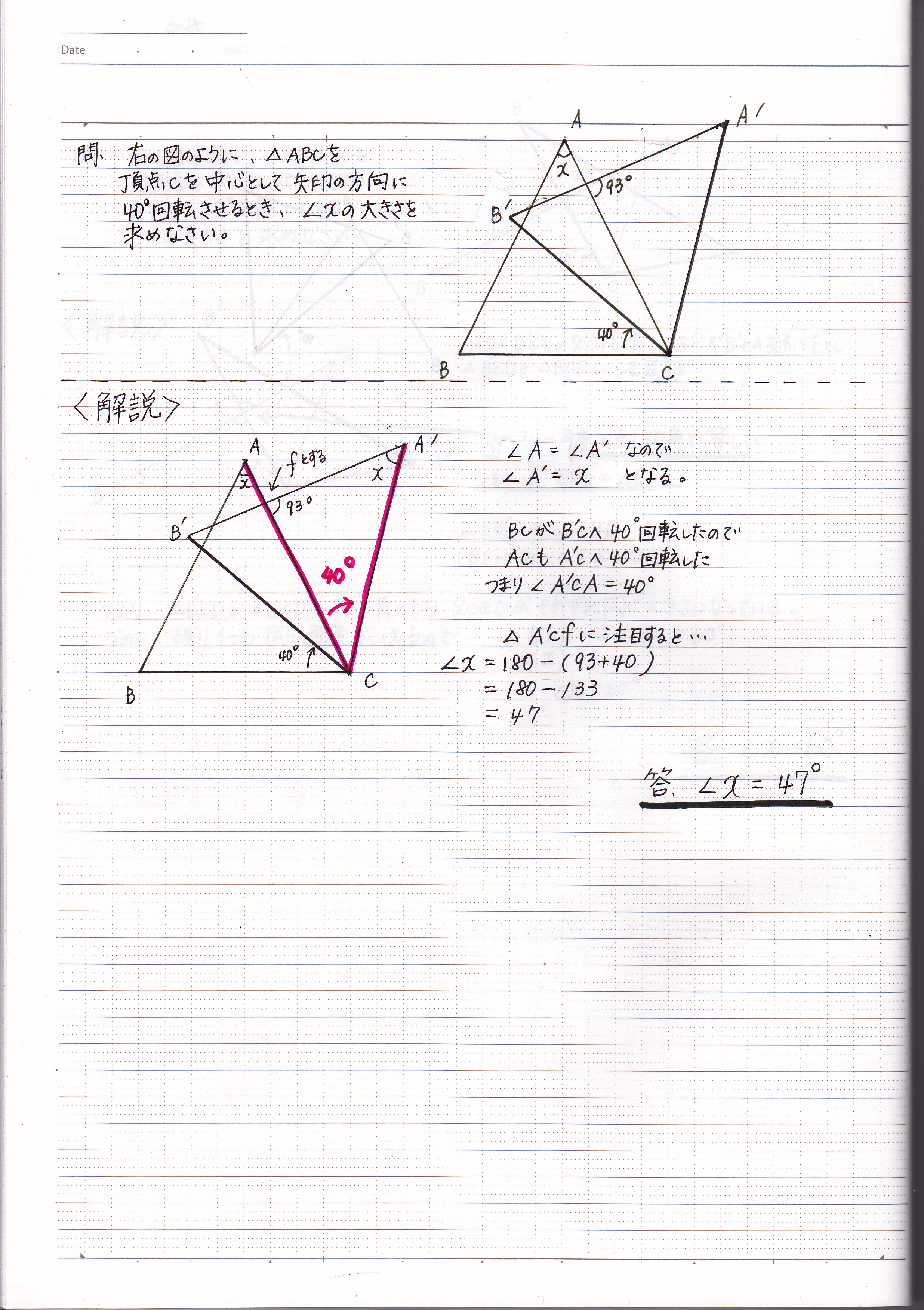



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方
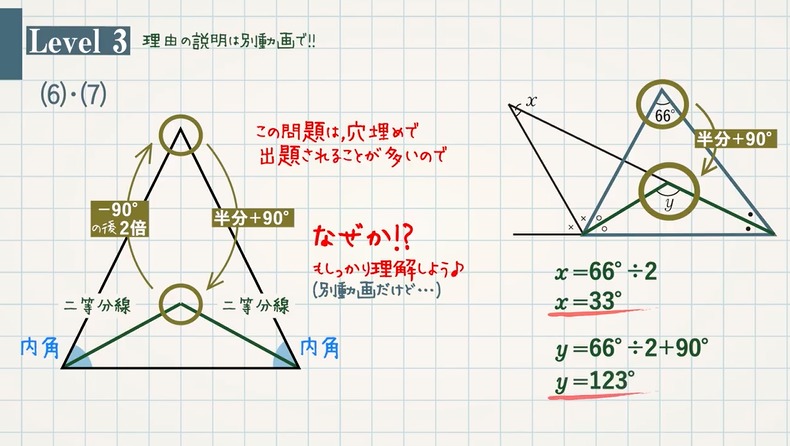



角度の計算 裏技まとめ 教遊者




直角三角形公式角度 直角三角形 斜辺と角度 三角形の計算 計算サイト翻譯此網頁 Rzcpe



1



3



0 件のコメント:
コメントを投稿